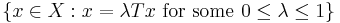Schauder fixed point theorem

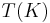The Schauder fixed point theorem is an extension of the Brouwer fixed point theorem to topological vector spaces, which may be of infinite dimension. It asserts that if K is a convex subset of a topological vector space V and T is a continuous mapping of K into itself so that T(K) is contained in a compact subset of K, then T has a fixed point.

A consequence, called Schaefer's fixed point theorem, is particularly useful for proving existence of solutions to nonlinear partial differential equations. Schaefer's theorem is in fact a special case of the far reaching Leray–Schauder theorem which was discovered earlier by Juliusz Schauder and Jean Leray. The statement is as follows. Let T be a continuous and compact mapping of a Banach space X into itself, such that the set

\{ x \in X�: x = \lambda T x \mbox{ for some } 0 \leq \lambda \leq 1 \}

is bounded. Then T has a fixed point.

Contents

History

The theorem was conjectured and proven for special cases, such as Banach spaces, by Juliusz Schauder in 1930. His conjecture for the general case was published in the Scottish book. In 1934, Tychonoff proved the theorem for the case when K is a compact convex subset of a locally convex space. This version is known as the Schauder–Tychonoff fixed point theorem. B. V. Singbal proved the theorem for the more general case where K may be non-compact; the proof can be found in the appendix of Bonsall's book (see references). The full result (without the assumption of local convexity) was finally proven by Robert Cauty in 2001.

See also

References

External links